NLP 处理方法
传统:基于规则
现代:基于统计机器学习
- HMM、CRF、SVM、LDA、CNN …
- “规则”隐含在模型参数里
我们希望词编码能够做到什么
词编码需要保证词的相似性
我们希望类似青蛙、蟾蜍这些词在词编码之后保持相似性

向量空间分布的相似性
从一个向量从一种语系转化成另一种语系的时候能够保持分布

向量空间子结构
$$ V_{king}-V_{Queen}=V_{Man}-V_{Women} \\ V_{Paris}-V_{France}=V_{German}-V_{Berlin} $$
我们希望原始文本信息能够得到保留,例如国王和女王之间的关系和男人与女人之间的关系应是特别接近的,法国和巴黎之间关系与德国和巴黎的关系也是接近的。
最终目标
词向量表示作为机器学习、特别是深度学习的输入和表示空间
在计算机中表示一个词
WordNet
WordNet是由Princeton大学的心理学家,语言学家和计算机工程师联合设计的一种基于认知语言学的英语词典。它不是光把单词以字母顺序排列,而且按照单词的意义组成一个“单词的网络”。它是一个覆盖范围宽广的英语词汇语义网。名词,动词,形容词和副词各自被组织成一个同义词的网络,每个同义词集合都代表一个基本的语义概念,并且这些集合之间也由各种关系连接。

WordNet 存在的问题
- 不能分别细节的差别
- 需要大量的人为劳动
- 主观
- 无法发现新词
- 难以精确计算词之间的相似度
离散表示:One-hot表示
假设有这么一个语料库
John likes to watch movies. Mary likes too.
John also likes to watch football games.
按照这个语料库可以构建出一个词典
{"John": 1, "likes": 2, "to": 3, "watch": 4, "movies'": 5,
"also":6, "football": 7, "games": 8, "Mary": 9, "too": 10}
可以看到这个词典里包含了10个单词,每个单词都有一个唯一的索引,在词典的顺序和在句子的顺序没有关联。
John的One-hot表示为
$$ [1,0,0,0,0,0,0,0,0,0] $$
同理likes的One-hot表示为
$$ [0,1,0,0,0,0,0,0,0,0] $$
离散表示:Bag of Words
文档的向量表示可以直接将各词的词向量表示加和
John likes to watch movies. Mary likes too.可表示为
$$ [1,2,1,1,1,0,0,0,1,1] $$
词权重
TF-IDF(Term Frequency - Inverse Document Frequency)
词$t$的IDF weight计算方式为
$$ log(1+\frac{N}{n_t}) $$
其中$N$为文档总数,$n_t$为含有词$t$的文档数
John likes to watch movies. Mary likes too.经过TF-IDF计算后文档向量可表示为
$$ [0.693,1.386,0.693,0.693,1.099,0,0,0,0.693,0.693] $$
Binary Weighting
只统计是否出现过,出现为1不出现为0,不统计出现次数
John likes to watch movies. Mary likes too.的向量记为
$$ [1,1,1,1,1,0,0,0,1,1] $$
离散表示:Bi-gram和N-gram
John likes to watch movies. Mary likes too.
John also likes to watch football games.
依旧以上面两句作为语料库,为了能够考虑到顺序的影响因素,为2-gram建立索引,得到词典如下
| word | index |
|---|---|
| John likes | 1 |
| likes to | 2 |
| to watch | 3 |
| watch movies | 4 |
| Mary likes | 5 |
| likes too | 6 |
| John also | 7 |
| also likes | 8 |
| watch football | 9 |
| football games | 10 |
John likes to watch movies. Mary likes too.的文档向量可表示为
$$ [1,1,1,1,1,1,0,0,0,0] $$
John also likes to watch football games.的文档向量可以表示为
$$ [0,1,1,0,0,0,1,1,1,1] $$
2-gram以每相邻的两个词建立词典,可以考虑到词的顺序对文档的影响,但是这样带来的问题是造成此表的膨胀。
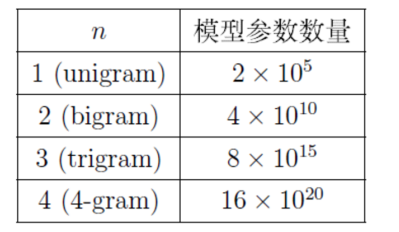
语言模型
判断一句话(词组合)出现的概率
$$ P(w_1,\cdots,w_m)=\prod_{i=0}^mP(w_i|w_1,\cdots,w_{i_1}) $$
Unigram/1-gram
$\begin{aligned} \mathrm{P}(\text { Mary likes too }) &=\mathrm{P}(\text { too } \mid \text { Mark, likes }) *\mathrm{P}(\text { likes } \mid \text { Mary })* \mathrm{P}(\text { Mary }) \\ &=\mathrm{P}(\text { too }) *\mathrm{P}(\text { likes })* \mathrm{P}(\text { Mary }) \end{aligned}$
Bigram/2-gram
$\begin{aligned} \mathrm{P}(\text { Mary likes too }) &=\mathrm{P}(\text { too } \mid \text { Mark, likes }) *\mathrm{P}(\text { likes } \mid \text { Mary })* \mathrm{P}(\text { Mary }) \\ &=\mathrm{P}(\text { too } \mid \text { likes }) *\mathrm{P}(\text { likes } \mid \text { Marry })^{*} \mathrm{P}(\text { Mary }) \end{aligned}$
离散表示的问题
无法衡量词向量之间的关系
$$ \begin{array}{ll} \text { 酒店 } & {[0,1,0,0,0,0,0,0,0,0]} \\ \text { 宾馆 } & {[0,0,0,0,1,0,0,0,0,0]} \\ \text { 旅舍 } & {[0,0,0,0,0,0,0,0,1,0]} \end{array} $$
使用各种度量(与或非、距离)都不合适,太过于稀疏,很难捕捉文本的含义
- 词表维度随着语料库增长膨胀
- n-gram词序列随语料库膨胀更快
- 数据稀疏问题
分布式表示(Distributed representation)
可以用一个词附近的其他词来表示该词
"You shall know a word by the company it keeps——(J. R. Firth 1957: 11)
现代统计自然语言处理中最有创见的想法之一

共现矩阵
Word-Document的共现矩阵主要用于发现主题(topic),用于主题模型,如LSA(Iatent Semantic Analysis)
局域窗中的Word-Word共现矩阵可以挖掘语法和语义信息
- I like deep learning
- I like NLP
- I enjoy flying
window length设为1(一般设置为5~10),使用对称的窗函数(左右window length都为1)
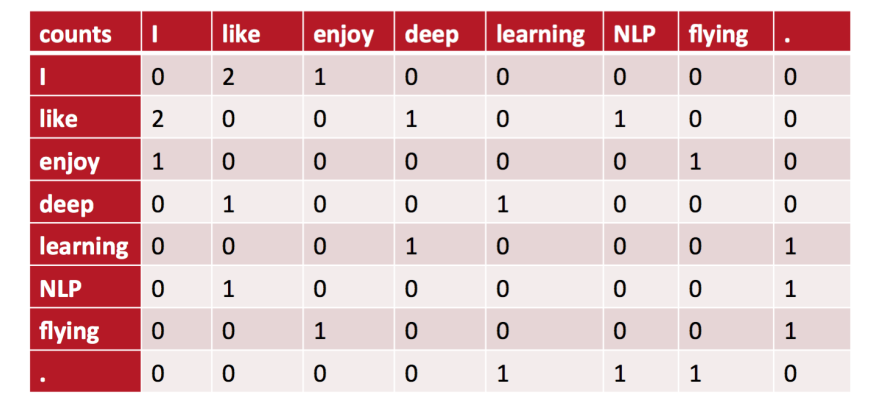
存在的问题
将共现矩阵行/列向量作为词向量
- 向量维数随着词典大小线性增长
- 存储整个词典的空间消耗非常大
- 一些模型如文本分类模型会面临稀疏性问题
- 模型会欠稳定
SVD降维
为了解决维度过大造成的稀疏性问题,最直接的方法是考虑构造低维稠密向量作为词的分布式表示(25~1000维),使用SVD对共现矩阵向量做降维

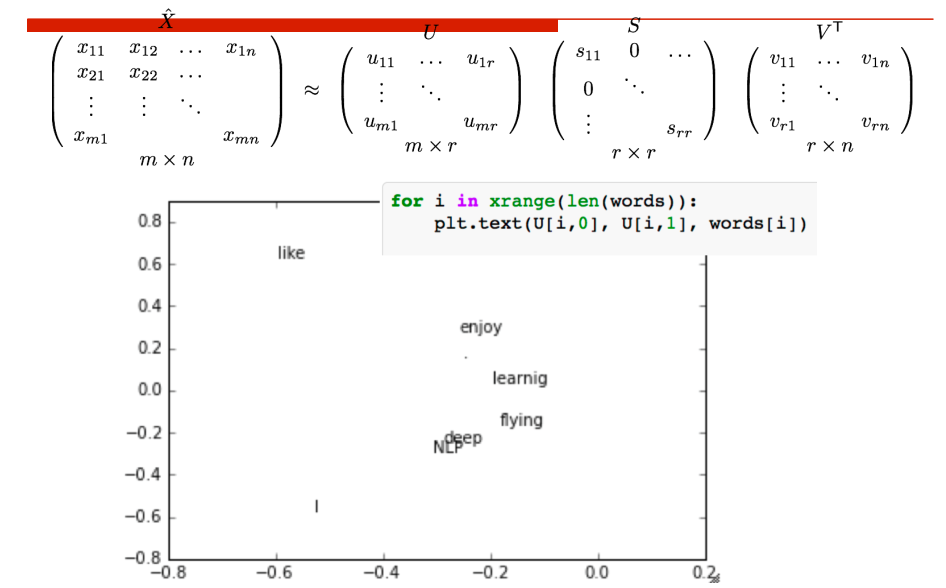
存在的问题
- 计算量随着语料库和词典增长膨胀太快,对$X(n\times n)$维的矩阵,计算量为$O(n^3)$,而对大型的语料库,n\~400k,语料库大小为1\~60Btoken
- 难以为词典中新加入的词分配词向量
- 与其他深度学习模型框架差异过大
NNLM(Neural Network Language model)
NNLM是word2vec的前身,直接从语言模型出发,将模型最优化过程转化为求词向量表示的过程。
目标函数
$$ L(\theta)=\sum_{i}\log P(w_t|w_{t-n+1},\cdots,w_{t-1}) $$
- 使用了非对称的前向窗函数,窗长度为n-1
- 滑动窗口遍历整个语料库求和,计算量正比与语料库大小
概率P满足归一化条件,这样不同位置t处的概率才能相加,即
$$ \sum_{w\in\{vocabulary\}}P(w|w_{t-n+1},\cdots,w_{t-1})=1 $$
