算法简介
梯度下降法(Gradient Descent)不是一种机器学习算法，而是是一种基于搜索的最优化方法，作用是最小化一个损失函数，例如在线性回归过程中，可以用梯度下降法来最小化损失函数，同样的，也可以用梯度上升法来最大化一个效用函数。
定义一个损失函数$J$，损失函数$J$的取值受$\theta$的影响，这里为了推导的方便，假设他是一个二次函数，如下图：
我们知道曲线$J$中某个点处的导数$\frac{dJ}{d\theta}$代表$\theta$单位变化时，$J$增大的方向，为了能够向减小的方向前进，则可以定义
$$ -\eta\frac{dJ}{d\theta} $$
$\eta$有着如下的定义：
- $\eta$ 称为学习率(learning rate)
- $\eta$ 的取值影响获得最优解的速度
- $\eta$ 取值如果不合适，可能得不到最优解
- $\eta$ 是梯度下降法的一个超参数
如果$\eta$ 太小，会减慢收敛学习的的速度，如果$\eta$ 太大，甚至导致不收敛。
同时有一个问题需要注意的，上述方法找到的极值点可能只是局部最优解，但并不是所有函数都有唯一的极值点，针对这个问题，解决方案是多次运行程序，初始化随机点，使用不同的随机点。从这里我们可以看到，梯度下降法中初始点也是一个超参数。
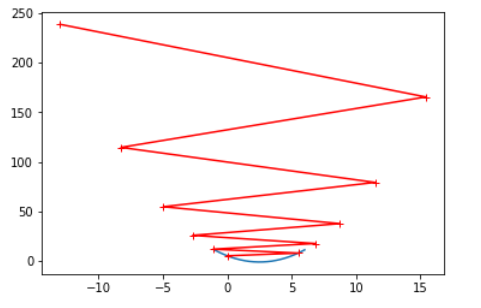
在简单线性回归中使用梯度下降法
首先使用模拟的数据
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
x = 2* np.random.random(size=100)
y = x * 3. + 4. + np.random.normal(size=100)
X = x.reshape(-1,1)
X.shape
# (100, 1)
y.shape
# (100,)
plt.scatter(x,y)
plt.show()
# 使用梯度下降法训练
def J(theta,X_b,y):
try:
return np.sum((y -X_b.dot(theta))**2) / len(X_b)
except:
return float('inf')
def dJ(theta, X_b, y):
res = np.empty(len(theta))
res[0] = np.sum(X_b.dot(theta) - y)
for i in range(1,len(theta)):
res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])
return res * 2 / len(X_b)
def gradient_depcent(X_b, y, initial_theta, eta, n_iters=1e4,psilon=1e-8):
theta=initial_theta
i_iter = 0
while i_iter < n_iters:
gradient=dJ(theta,X_b,y)
last_theta=theta
theta = theta-eta * gradient
if(abs(J(theta,X_b,y)-J(last_theta,X_b,y ))<epsilon):
break
i_iter += 1
return theta
X_b = np.hstack([np.ones((len(X),1)),X])
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01
theta = gradient_depcent(X_b,y,initial_theta,eta)
theta
# array([4.02145786, 3.00706277])在多元线性回归中使用梯度下降法
推导
在前面我们知道多元线性回归问题中损失函数$J=\sum\limits_{i=1}^m(y^{(i)}-\hat{y}^{(i)})^2$，参数为$\theta = (\theta_0,\theta_1,\theta_2,...,\theta_n)$，在前面$-\eta\frac{dJ}{d\theta}$在此处应该写成$-\eta\nabla J$的形式，其中
$$ \nabla J = (\frac{\partial J}{\partial \theta_0},\frac{\partial J}{\partial \theta_1},\ldots,\frac{\partial J}{\partial \theta_n}) $$
在多元线性回归中，目标是为了使得$\sum\limits_{i=1}^m(y^{(i)}-\hat{y}^{(i)})^2$尽可能的小，又因为
$$ \hat{y}^{(i)}=\theta_0+\theta_1X_1^{(i)}+…+\theta_nX_n^{(i)} $$
所以目标转化为使得
$$ \sum_{i=1}^{m}\left(y^{(i)}-\theta_{0}-\theta_{1} X_{1}^{(i)}-\ldots-\theta_{n} X_{n}^{(i)}\right)^{2} $$
尽可能地小
$$ \nabla J(\theta)=\left(\begin{array}{c} \partial J / \partial \theta_{0} \\ \partial J / \partial \theta_{1} \\ \partial J / \partial \theta_{2} \\ \cdots \\ \partial J / \partial \theta_{n} \end{array}\right) =\left(\begin{array}{c} \sum\limits_{i=1}^{m} 2\left(y^{(i)}-X_{b}^{(i)} \theta\right) \cdot(-1) \\ \sum\limits_{i=1}^{m} 2\left(y^{(i)}-X_{b}^{(i)} \theta\right) \cdot\left(-X_{1}^{(i)}\right) \\ \sum\limits_{i=1}^{m} 2\left(y^{(i)}-X_{b}^{(i)} \theta\right) \cdot\left(-X_{2}^{(i)}\right) \\ \cdots \\ \sum\limits_{i=1}^{m} 2\left(y^{(i)}-X_{b}^{(i)} \theta\right) \cdot\left(-X_{n}^{(i)}\right) \end{array}\right) =2 \cdot\left(\begin{array}{c} \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \\ \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{1}^{(i)} \\ \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{2}^{(i)} \\ \cdots \\ \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{n}^{(i)} \end{array}\right) $$
如果我们令目标函数乘以一个常数$\frac{1}{m}$，得到$J(\theta)=\frac{1}{m}\sum\limits_{i=1}^m(y^{(i)}-\hat{y}^{(i)})^2=MSE(y,\hat{y})$，此时则有：
$$ \nabla J(\theta)=\frac{2}{m}\left(\begin{array}{c} \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \\ \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{1}^{(i)} \\ \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{2}^{(i)} \\ \cdots \\ \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{n}^{(i)} \end{array}\right) $$
实现(以波士顿房价数据为例)
记得使用梯度下降法之前需要对数据进行归一化处理
# 导入数据
import numpy as np
from sklearn import datasets
boston = datasets.load_boston()
x = boston.data
y = boston.target
x = x[y<50.0]
y = y[y<50.0]
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state = 666)
# 数据归一化
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(x_train)
from LinearRegression import LinearRegression
x_train_standard = standardScaler.transform(x_train)
lin_reg = LinearRegression()
lin_reg.fit_gd(x_train_standard,y_train)
x_test_standard = standardScaler.transform(x_test) # 需要对测试集也进行同样的归一化
lin_reg.score(x_test_standard,y_test)
# 0.8129873310487505线性回归中梯度下降法的向量化
在前面我们得到了$\nabla J(\theta)$的表达式，为了使得计算效率得到提升，对其进行向量化处理
$$ \nabla J(\theta)=\frac{2}{m}\left(\begin{array}{c} \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \\ \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{1}^{(i)} \\ \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{2}^{(i)} \\ \cdots \\ \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{n}^{(i)} \end{array}\right) $$
$$ = \frac{2}{m} \cdot \left(X_{b}^{(1)} \theta-y^{(1)}, \quad X_{b}^{(2)} \theta-y^{(2)}, \quad X_{b}^{(3)} \theta-y^{(3)}, \quad \ldots,\quad X_{b}^{(m)} \theta-y^{(m)}\right)\ \cdot \left(\begin{array}{ccccc} X_{0}^{(1)} & X_{1}^{(1)} & X_{2}^{(1)} & \ldots & X_{n}^{(1)} \\ X_{0}^{(2)} & X_{1}^{(2)} & X_{2}^{(2)} & \ldots & X_{n}^{(2)} \\ X_{0}^{(3)} & X_{1}^{(3)} & X_{2}^{(3)} & \ldots & X_{n}^{(3)} \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ X_{0}^{(m)} & X_{1}^{(m)} & X_{2}^{(m)} & \ldots & X_{n}^{(m)} \end{array}\right) $$
$$ =\frac{2}{m}\cdot(X_b\theta-y)^T\cdot X_b=\frac{2}{m}\cdot X_b^T\cdot (X_b\theta-y) $$
整理可得
$$ \nabla J(\theta)=\frac{2}{m}\cdot X_b^T\cdot (X_b\theta-y) $$
随机梯度下降法
推导
前面我们得到批量梯度下降法(Batch Gradient Descent)，这里考虑另一种梯度下降法：随机梯度下降法(Stochastic Gradient Descent)
在批量梯度下降法中我们知道
$$ \nabla J(\theta)=\frac{2}{m}\left(\begin{array}{c} \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \\ \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{1}^{(i)} \\ \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{2}^{(i)} \\ \cdots \\ \sum\limits_{i=1}^{m}\left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{n}^{(i)} \end{array}\right) $$
每次运我们都需要对所有$m$个样本进行计算，之后再取平均，这样运行起来是十分慢的，那么我们自然而然可以想，是不是可以每次只对其中一个样本进行计算，基于这样的想法，可以将上式变成
$$ 2\cdot \left(\begin{array}{c} \left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{0}^{(i)} \\ \left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{1}^{(i)} \\ \left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{2}^{(i)} \\ \cdots \\ \left(X_{b}^{(i)} \theta-y^{(i)}\right) \cdot X_{n}^{(i)} \end{array}\right) =2 \cdot\left(X_{b}^{(i)}\right)^{T} \cdot\left(X_{b}^{(i)} \theta-y^{(i)}\right) $$
在随机梯度下降法中，由于每次搜索不能保证得到的方向是损失函数减小的方向，更不能保证是下降最快的方向，所以搜索路径会出现如下图的情况。
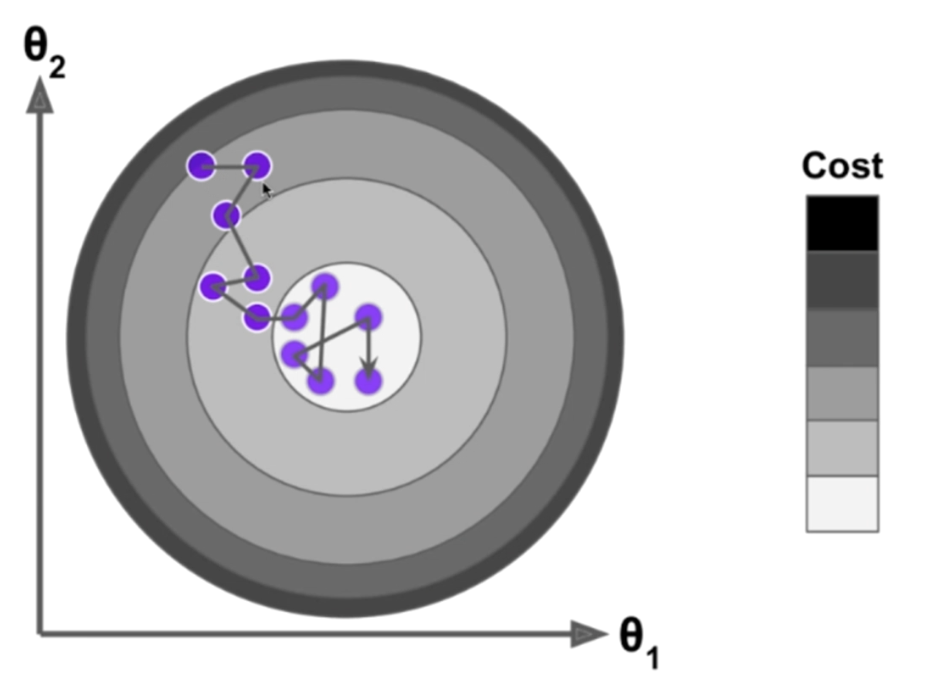
在随机梯度下降法中，学习率$ \eta $的取值比较重要，我们希望随着循环次数的增加，$\eta$值越来越小，那么有
$$ \eta=\frac{a}{i_{-} \text {iters }+b} $$
实现
# 梯度运算公式
def dJ_sgd(theta, X_b_i, y_i):
return X_b_i.T.dot(X_b_i.dot(theta)-y_i)*2.
def sgd(X_b,y,initial_theta,n_iters):
t0 = 5
t1 = 50
def learning_rate(t):
return t0 / (t + t1)
theta = initial_theta
for cur_iter in range(n_iters):
rand_i = np.random.randint(len(X_b))
gradient = dJ_sgd(theta, X_b[rand_i],y[rand_i])
theta = theta - learning_rate(cur_iter)*gradient
return theta
m = 100000
x = np.random.normal(size=m)
X = x.reshape(-1,1)
y = 4. * x +3. + np.random.normal(0,3,size=m)
X_b = np.hstack([np.ones((len(x),1)),X])
initial_theta = np.zeros(X_b.shape[1])
X_b = np.hstack([np.ones((len(X),1)),X])
initial_theta = np.zeros(X_b.shape[1])
# 只检查三分之一样本
theta = sgd(X_b,y,initial_theta,n_iters=len(X_b)//3)
theta
# array([2.9952686 , 3.94910815])scikit-learn中使用随机梯度下降法
# 导入数据
from sklearn import datasets
boston = datasets.load_boston()
x = boston.data
y = boston.target
x = x[y<50.0]
y = y[y<50.0]
# 分割数据集
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state=666)
# 归一化处理
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(x_train)
x_train_standard = standardScaler.transform(x_train)
x_test_standard = standardScaler.transform(x_test)
# 使用随机梯度下降法
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor()
sgd_reg.fit(x_train_standard,y_train)
sgd_reg.score(x_test_standard,y_test)
# 0.7979411957717837
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(n_iter_no_change=100)
sgd_reg.fit(x_train_standard,y_train)
sgd_reg.score(x_test_standard,y_test)
# 0.8009888207151269