算法简介
- 解决回归问题
- 思想简单,实现容易
- 许多强大的非线性模型的基础
- 结果具有很强的解释性
- 蕴含机器学习中很多的重要思想
线性回归算法可以简单概括为,寻找一条直线,最大程度地“拟合”样本特征和样本输出标记之间的关系。

推导
假设我们找到了最佳拟合的直线方程$y=ax+b$,则对于每个样本点$x^{(i)}$ ,根据我们的直线方程,预测值就为$\hat{y}^{(i)}=ax^{(i)}+b$,我们希望真值$y^{(i)}$与$\hat{y}^{(i)}$之间的差距尽量的小,可以用$(y^{(i)}-\hat{y}^{(i)})^2$来衡量真实值与预测值之间的差距,考虑到所有的样本,则是
$$ \sum\limits_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})^2 $$
其中
$$ \hat{y}^{(i)}=ax^{(i)}+b $$
我们想使得上述函数尽可能小,那么我们的问题可以转化为找到$a和b$使得$\sum\limits_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})^2$尽可能小,我们一般把这个函数称为损失函数(loss function)或者效用函数(utillity function),通过分析问题,确定问题的损失函数或者效用函数,通过优化损失函数或者效用函数,可以获得机器学习的模型,对于几乎所有的参数学习的算法,都是这样的套路,比如线性回归、多项式回归、逻辑回归和SVM等。
对于上述的式子,可以得到整理后的损失函数为:
$$ \sum\limits_{i=1}^{m}(y^{(i)}-ax^{(i)}-b)^2 $$
这是一个典型的最小二乘法问题,即最小化误差的平方,可以得到
$$ a=\frac{\sum_\limits{i=1}^{m}\left(x^{(i)}-\bar{x}\right)\left(y^{(i)}-\bar{y}\right)}{\sum\limits_{i=1}^{m}\left(x^{(i)}-\bar{x}\right)^{2}} $$
$$ b=\overline{y}-a\overline{x} $$
了便于算法的运行效率,我们尝试转化成向量化计算的形式,即$\sum\limits_{i=1}^{m}w^{(i)}v^{(i)}$这种形式,对于分子,令$w^{(i)}=x^{(i)}-\bar{x},v^{(i)}=y^{(i)}-\bar{y}$,令$w=(w^{(1)}),w^{(2)},....,w^{(n)}),v=(v^{(1)}),v^{(2)},....,v^{(n)})$,则$\sum\limits_{i=1}^{m}w^{(i)}v^{(i)}$可以看作是$w\cdot v $
简单实现
import numpy as np
import matplotlib.pyplot as plt
x = np.array([1.,2.,3.,4.,5.])
y = np.array([1.,3.,2.,4.,5.])
x_mean = np.mean(x)
y_mean = np.mean(y)
num = 0.0
d = 0.0
for x_i, y_i in zip(x,y):
num += (x_i - x_mean)*(y_i - y_mean)
d += (x_i - x_mean)**2
a = num/d
b = y_mean - a * x_mean
y_hat = a * x + b
plt.scatter(x,y)
plt.plot(x,y_hat,color = 'r')
plt.axis([0,6,0,6])
plt.show()
自己封装线性回归算法
#SimpleLinearRegression.py
import numpy as np
from metrics import r2_score
class SimpleLinearRegression:
def __init__(self):
"""初始化Simple Linear Regression模型"""
self.a_ = None
self.b_ = None
def fit(self, x_train, y_train):
"""根据训练数据集x_train, y_train训练Simple Linear Regression模型"""
assert x_train.ndim == 1, \
"Simple Linear Regressor can only solve single feature training data."
assert len(x_train) == len(y_train), \
"the size of x_train must be equal to the size of y_train"
x_mean = np.mean(x_train)
y_mean = np.mean(y_train)
self.a_ = (x_train - x_mean).dot(y_train - y_mean) / (x_train - x_mean).dot(x_train - x_mean)
self.b_ = y_mean - self.a_ * x_mean
return self
def predict(self, x_predict):
"""给定待预测数据集x_predict,返回表示x_predict的结果向量"""
assert x_predict.ndim == 1, \
"Simple Linear Regressor can only solve single feature training data."
assert self.a_ is not None and self.b_ is not None, \
"must fit before predict!"
return np.array([self._predict(x) for x in x_predict])
def _predict(self, x_single):
"""给定单个待预测数据x,返回x的预测结果值"""
return self.a_ * x_single + self.b_
def score(self, x_test, y_test):
"""根据测试数据集 x_test 和 y_test 确定当前模型的准确度"""
y_predict = self.predict(x_test)
return r2_score(y_test, y_predict)
def __repr__(self):
return "SimpleLinearRegression()"from SimpleLinearRegression import SimpleLinearRegression
reg = SimpleLinearRegression()
reg.fit(x,y)
# SimpleLinearRegression()
reg.predict(np.array([x_predict]))
# array([5.7])
y_hat = reg.predict(x)
plt.scatter(x,y)
plt.plot(x,y_hat,color='g')
plt.axis([0,6,0,6])
plt.show()
衡量回归算法的标准
对于上述算法中,要求找到$a$和$b$,使得损失函数$\sum\limits_{i=1}^{m}(y_{train}^{(i)}-ax_{train}^{(i)}-b)^2$,尽可能小,等价于使得$\sum\limits_{i=1}^{m}(y_{train}^{(i)}-\hat{y}_{train}^{(i)})^2$尽可能小,那么我们是否也可以用$\sum\limits_{i=1}^{m}(y_{test}^{(i)}-\hat{y}_{test}^{(i)})^2$作为衡量回归算法的标准呢,仔细一想这样是不行的,这种计算方式与$m$的相关性很大,由此我们推出了其他几种误差的计算方法,主要有以下几个
均方误差MSE(Mean Squared Error)
$$ \frac{1}{m}\sum\limits_{i=1}^m(y_{test}^{(i)}-\hat{y}_{test}^{(i)})^2 $$
均方根误差RMSE(Root Mean Squared Error)
$$ \sqrt{\frac{1}{m}\sum\limits_{i=1}^m(y_{test}^{(i)}-\hat{y}_{test}^{(i)})^2}=\sqrt{MSE_{test}} $$
平均绝对误差MAE(Mean Absolute Error)
$$ \frac{1}{m}\sum_{i=1}^m\vert y_{test}^{(i)}-\hat{y}_{test}^{(i)}\vert $$
R Squared
$$ R^2=1-\frac{SS_{residual}}{SS_{total}}=1-\frac{\sum\limits_i(\hat{y}^{(i)}-y^{(i)})^2}{\sum\limits_i(\overline{y}-y^{(i)})^2} $$
其中$SS_{residual}$表示Residual Sum of Squares,$SS_{total}$表示Total Sum of Squares,这个评价方法也是scikit-learn中线性回归算法中score方法调用的评价指标。对于$\sum\limits_i(\hat{y}^{(i)}-y^{(i)})^2$我们可以理解成使用我们的模型预测产生的错误,对于$\sum\limits_i(\overline{y}-y^{(i)})^2$可以理解为使用$y=\overline{y}$预测产生的错误,有以下几点需要清楚:
- 对于$R^2$来说,总是小于等于1的
- $R^2$越大越好,当模型预测不犯任何错误时,$R^2=1$
- 当我们的模型等于基准模型时,$R^2=0$
- 如果$R^2<0$,说明学习的模型还不如基准模型,此时说明我们的数据可能不存在任何线性关系
另外,可以推导得到R Squared、MSE和方差之间的关系
$$ R^2=1-\frac{\sum\limits_i(\hat{y}^{(i)}-y^{(i)})^2}{\sum\limits_i(\overline{y}-y^{(i)})^2}=1-\frac{(\sum\limits_{i=1}^m(\hat{y}^{(i)}-y^{(i)})^2)/m}{(\sum\limits_{i=1}^m(y^{(i)}-\overline{y})^2)/m}=1-\frac{MSE(\hat{y},y)}{Var(y)} $$
以波士顿房价数据为例对线性回归结果进行评价
from sklearn import datasets
boston = datasets.load_boston()
x = boston.data[:,5] #只使用房间数量这个特征
x.shape
# (506,)
y = boston.target
plt.scatter(x,y)
plt.show()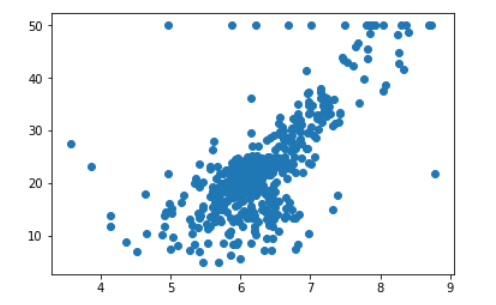
发现存在边界值,需要对其进行清除
# 去掉边界点
x = x[y<50.0]
y = y[y<50.0]
plt.scatter(x,y)
plt.show()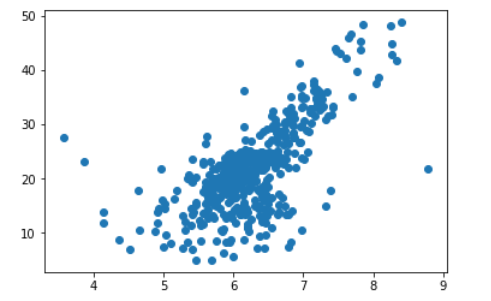
# 使用自己封装的两个函数
from model_selection import train_test_split
from SimpleLinearRegression import SimpleLinearRegression
x_train,x_test,y_train,y_test = train_test_split(x,y,seed = 666)
reg = SimpleLinearRegression()
reg.fit(x_train,y_train)
y_predict = reg.predict(x_test)
plt.scatter(x_train,y_train)
plt.plot(x_train,reg.predict(x_train),color='r')
plt.show()
# MSE
mse_test = np.sum((y_predict - y_test)**2) / len(y_test)
# 24.156602134387438
# RMSE
from math import sqrt
rmse_test = sqrt(mse_test)
# 4.914936635846635
# MAE
mae_test = np.sum(np.absolute(y_predict - y_test) / len(y_test))
# 3.543097440946387
# R square
r_square = 1 - mean_squared_error(y_test,y_predict) / np.var(y_test)
# 0.6129316803937322
# 也可以使用scikit-learn中的函数来计算MSE和MAE
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
mean_squared_error(y_test,y_predict)
# 24.156602134387438
mean_absolute_error(y_test,y_predict)
3.5430974409463873
1 条评论
内容的丰富性和深度让人仿佛置身于知识的海洋,受益匪浅。